Table of Contents

System Information

Definition Index

• LISP-INFERENCE

  • INFERENCE

  No documentation provided.

  • EXTERNAL SPECIAL-VARIABLE

    *MAX-PROPOSITIONS*

    Source

    Max number of propositions to generate truth table, more than this will generate a program-error.

  • EXTERNAL SPECIAL-VARIABLE

    *OUTPUT-STREAM*

    Source

    Default stream to write the results

  • EXTERNAL SPECIAL-VARIABLE

    *VALID-OPERATORS*

    Source

    No documentation provided.
  • EXTERNAL FUNCTION

    ->

    • P
    • Q

    Source

    Notation alias for conditional

  • EXTERNAL FUNCTION

    <->

    • P
    • Q

    Source

    Notation alias for biconditional

  • EXTERNAL FUNCTION

    <=>

    • P
    • Q

    Source

    Biconditional binary operator

  • EXTERNAL FUNCTION

    =>

    • P
    • Q

    Source

    Conditional binary operator

  • EXTERNAL FUNCTION

    ABSORPTION

    • EXP

    Source

    Absorption inference rule ::
      (=> p q) => (=> p (^ p q))

  • EXTERNAL FUNCTION

    ADDITION

    • EXP
    • P

    Source

    Addition in inference rule ::
       p => (v p q)

  • EXTERNAL FUNCTION

    BICONDITIONALP

    • EXP

    Source

    Verify if the expression is a biconditional

  • EXTERNAL FUNCTION

    BINARY-OPERATIONP

    • EXP

    Source

    No documentation provided.
  • EXTERNAL FUNCTION

    CONJUNCTION

    • EXP
    • P

    Source

    Conjunction inference rule ::
       p => (^ p q)

  • EXTERNAL FUNCTION

    CONJUNCTIONP

    • EXP

    Source

    Verify if the expression is a conjunction

  • EXTERNAL FUNCTION

    DE-MORGAN

    • EXP

    Source

    De Morgan equivalence rule ::
      (~ (^ p q)) <=> (v (~ p) (~ q))
      (^ p q) <=> (~ (v (~ p) (~ q)))
      (~ (v p q)) <=> (^ (~ p) (~ q))
      (v p q) <=> (~ (^ (~ p) (~ q)))

  • EXTERNAL FUNCTION

    DISJUNCTIONP

    • EXP

    Source

    Verify if the expression is a disjunction

  • EXTERNAL FUNCTION

    DOUBLE-NEGATION

    • EXP

    Source

    Double negation equivalence rule ::
       (~ (~ p)) <=> p

  • EXTERNAL FUNCTION

    EQUAL-EXPRESSION

    • EXP1
    • EXP2

    Source

    Check if the two expressions have the same truth tables.
    The result is the same as check if (exp1 <=> exp2) results in
    a tautology.

  • EXTERNAL FUNCTION

    EVAL-EXPRESSION

    • EXP

    Source

    Return the boolean values of EXP
    Ex.: (eval-expression (=> p q))
    'TFTT'
    

  • EXTERNAL FUNCTION

    IMPLICATION

    • EXP

    Source

    Implication equivalence ::
      (=> p q) <=> (v (~ p) q)

  • EXTERNAL FUNCTION

    IMPLICATIONP

    • EXP

    Source

    Verify if the expression is an implication

  • EXTERNAL FUNCTION

    INFIX-TO-PREFIX

    • EXP

    Source

    INFIX-TO-PREFIX translate a infix expression to a prefix expression.
    
    This function assumes that exp it is not ambiguous.
    In that case, use a completly 'parenthesed' expression
    
    Returns a new prefixed list.
    

  • EXTERNAL FUNCTION

    MAIN

    Source

    No documentation provided.
  • EXTERNAL FUNCTION

    MAKE-BICONDITIONAL

    • P
    • Q

    Source

    No documentation provided.
  • EXTERNAL FUNCTION

    MAKE-CONJUNCTION

    • P
    • Q

    Source

    No documentation provided.
  • EXTERNAL FUNCTION

    MAKE-DISJUNCTION

    • P
    • Q

    Source

    No documentation provided.
  • EXTERNAL FUNCTION

    MAKE-IMPLICATION

    • P
    • Q

    Source

    No documentation provided.
  • EXTERNAL FUNCTION

    MAKE-NEGATION

    • P

    Source

    No documentation provided.
  • EXTERNAL FUNCTION

    MODUS-PONENS

    • EXP

    Source

    Modus Ponens inference rule ::
      (^ (=> p q) p) => q

  • EXTERNAL FUNCTION

    MODUS-TOLLENS

    • EXP

    Source

    Modus Tollens inference rule ::
       (^ (=> p q) (~ p)) => (~ q)

  • EXTERNAL FUNCTION

    NEGATIONP

    • EXP

    Source

    Verify if the expression is a negation

  • EXTERNAL FUNCTION

    OPERATIONP

    • EXP
    • OP

    Source

    Based a 'op that can be a symbol, verify if the list
       can be a operation of 'op

  • EXTERNAL FUNCTION

    PARSE-LOGIC

    • INPUT

    Source

    PARSE-LOGIC receive a INPUT as string and use a pratt parser to convert in infix notation

  • EXTERNAL FUNCTION

    PREFIX-TO-INFIX

    • EXP

    Source

    No documentation provided.
  • EXTERNAL FUNCTION

    PRINT-TRUTH-TABLE

    • EXP

    Source

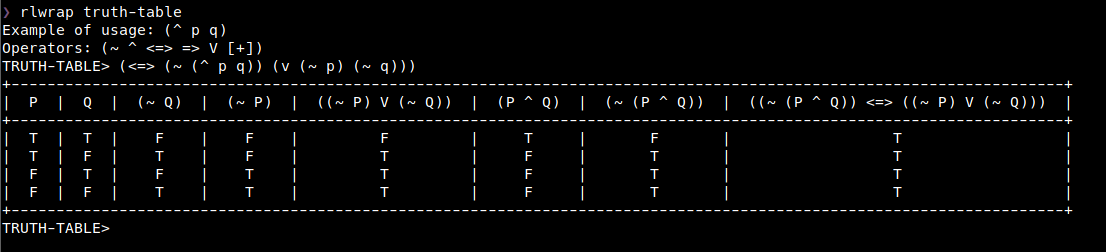
    Given a EXP with prefixed notation generate
       a pretty truth-table for each grouped case.

  • EXTERNAL FUNCTION

    PROPOSITIONP

    • SYMBOL

    Source

    Check if the given SYMBOL can be a proposition (letters)

  • EXTERNAL FUNCTION

    SIMPLIFICATION-FIRST

    • EXP

    Source

    Simplification with first operand rule ::
      (^ p q) => p

  • EXTERNAL FUNCTION

    SIMPLIFICATION-SECOND

    • EXP

    Source

    Simplification with second operand rule ::
      (^ p q) => q

  • EXTERNAL FUNCTION

    SYLLOGISM-DISJUNCTIVE

    • EXP

    Source

    Syllogism Disjunctive inference rule ::
       (^ (v p q) (~ p)) => q

  • EXTERNAL FUNCTION

    SYLLOGISM-HYPOTHETICAL

    • EXP

    Source

    Syllogism Hypothetical inference rule ::
      (^ (=> x y) (=> y z)) => (=> x z)
      (^ (=> y z) (=> x y)) => (=> x z)

  • EXTERNAL FUNCTION

    UNARY-OPERATIONP

    • EXP

    Source

    No documentation provided.
  • EXTERNAL FUNCTION

    V

    • P
    • Q

    Source

    Disjunction binary operator

  • EXTERNAL FUNCTION

    VALID-OPERATIONP

    • EXP

    Source

    No documentation provided.
  • EXTERNAL FUNCTION

    [+]

    • P
    • Q

    Source

    XOR operator or exclusive disjunction operator

  • EXTERNAL FUNCTION

    ^

    • P
    • Q

    Source

    Conjuction binary operator

  • EXTERNAL FUNCTION

    ~

    • P

    Source

    Not unary operator

  • EXTERNAL MACRO

    TRUTH

    • EXP

    Source

    An easy way to generate a truth table

  • EXTERNAL MACRO

    TRUTH-INFIX

    • &REST
    • EXP

    Source

    An easy and infix way of EXP generate a truth table.
       Ex.: (truth-infix (p ^ q))