Essas notas se concentram toda a revisão, resumo e exercícios para o Cápitulo II do livro Discrete-Time Digital Processing do Oppenheim: Sinais e Sistemas Lineares Invariantes no Tempo. Esse material refere-se a disciplina de Processamento Digital de Sinais.
Descrição
As últimas aulas de PDS foram dadas a respeito sobre as definições básicas de sinal e sistema. Outras propriedades foram faladas também como:
- Memoria
- Linearidade
- Sistemas Lineares Invariantes no Tempo
- Causalidade
- Estabilidade
Também foi comentado sobre entidades como media móvel, delta de Dirac (contínuo) e delta de Kronecker (discreto).
Existem três tipos de sistemas: contínuo, discretos no tempo e digitais.
Sistemas computacionais são digitais, no entanto na teoria de PDS será estudado sistemas discretos no tempo. A diferença entre eles é que os valores que um sinal pode assumir é contínuo, embora os valores do tempo (abscissas) são discretos.
Conceitos
Os conceitos principais para a disciplina de Processamento Digitais de Sinais (PDS), envolve os conceitos já definidos na disciplina de Sistemas Lineares (que não fiz completamente). Os conceitos elementares envolvem Sinais e Sistemas de Sinais, dos quais derivam-se os domínios: contínuo, discreto no tempo e digital.
Sinais contínuos tem seu domínio e contra-domínio contínuo, referenciado muitas vezes como sinais analógicos. Sinais discretos no tempo possui o tempo discreto, mas a amplitude contínua. Sinais digitais são ambos discretos em tempo e amplitude.
As transformações sucessivas entre esses tipos de sinais são chamados de amostragem e quantização. A transformação de um sinal em outro é chamado de sistema.
Sinais
Sinal é nada mais que uma função com uma interpretação física: uma entidade mensurável. No domínio discreto no tempo recebe uma notação especial \(f[n]\) enquanto no contínuo geralmente é \(f(t)\). Sinais discretos podem ser interpretados também com uma sequência numérica, com seus valores associados em \(n \in \mathbb{N}\).
Um sinal muito importante é o impulso unitário, definido como o delta de kronecker para o caso discreto. \(\delta[n = 0] = 1\) e \(\delta[n \neq 0]=0 \).
Como será visto na discussão de sistemas lineares, uma dos mais importantes aspectos de uma sequência de impulsos é que um sequência arbitrária pode ser descrita como uma soma ponderada de impulsos atrasados.
Além disso, um sinal discreto pode ser representando como um sinal contínuo com uma amostragem matemática definida como:
Representa a \(n\)-ésima componente do sinal contínuo \(x_c(t)\) obtida de um processo de amostragem periódica.
Sendo \(T\) o período de amostragem, tal que \(T \in \mathbb{R} \) e \(n \in \mathbb{N} \).
Sistemas
Sistema tem como entrada um sinal e resposta um novo sinal. De forma um tanto detalhada, é dita que: `Fenômeno físico que exerce transformações sobre os sinais, modificando o conteúdo de informação nele contida.'
Sinal unitário
Sinal unitário é definido como delta de kronecker para o domínio discreto.
Delta de Kronecker
O delta de kronecker é definido como \(\delta[0]=1\) e para todos outros igual a 0.
Sinal degrau
O sinal degrau é \(u[n \geq 0] = 1\) e zero para todo o resto. Há algumas implicações do sinal degrau com o sinal unitário, como de fato no exemplo no sistema acumulador, recebendo o sinal unitário de entrada, vamos criar o sinal degrau.
Propriedades de sistemas
Memória
Um sistema pode ser definido com memória ou sem memória. Sistemas ideais sem memória não dependem de entradas passadas. Por exemplo o sistema média móvel é um sistema com memória pois deve armazenar \(n\) entradas para calcular a cada ponto. Um amplificador pode ser implementado sem memória, no entanto amplificadores reais geralmente são implementados com memória por alguma razão obscura que ainda não sei 1.
Linearidade
Se provado as condições de superposição, é dito que o sistema é linear. Vale lembrar que as condições de superposição são os axiomas da aditividade (Eq. 1) e homogeneidade (Eq. 1) .
Invariância no Tempo
Sistemas invariantes no tempo são aqueles quando o sinal atrasado na entrada ou atrasado na saida, gera o mesmo sistema. Para provar se é SLIV, é necessário provar para todos os possíveis atrasos. Para refutar, é necessário apenas um contra-exemplo.
Matematicamente descrito como:
Por exemplo, o sistema acumulador é invariante no tempo.
Causalidade
A causalidade define que um sistema causal é aquele que não depende de entradas futuras. Isto é, um sistema é causal se, para todo \(n_0\), o valor da saída em \(n=n_0\), depende somente dos valores da entrada en \(n \leq n_0\).
O acumulador, por exemplo, é causal pois depende apenas das entradas anteriores para calcular os próximos sinais.
Estabilidade
Para um sistema ser estável ele precisa ter uma saída e entrada limitada 2.
Na qual \(B_x, B_y > 0\) são números positivos finitos.
- O conceito de estabilidade de um sistema não dependente do tipo de entrada.
- Um dado sistema pode produzir uma saída limitada apenas para um número restrito de entradas limiitadas. Nesse caso, o sistema não é estável.
- Sistemas estáveis produzem saídas limitadas para todo tipo de entrada limitada.
Convolução de Sinais Discreto no Tempo
Sistemas convolucionais. Uma convolução é realizada entre dois sinais e gera um novo sinal. Uma das interpretações intuitivas é que ao transladar uma das funções em relação a outra, é calculado a média móvel em relação a área de intersecção desses dois sinais. Para calcular a convolução de sinais é necessário realizar algumas operações primárias, sendo que de fato a convolução é uma soma infinita de impulsos ponderados deslocados no tempo.
Primeiramente devemos entender que sistemas lineares invariantes no tempo podem ser caracterizados completamente por sua resposta ao impulso. Através de alguns artifícios matemáticos, obtem-se:
Dado que pela invariância no tempo: \(T\{\delta[n]\}=h[n] \Rightarrow T\{\delta[n-k]\}=h[n-k]\).
Os passos para calcular a operação de convolução são:
- Refletir \(h[k]\) em torno da origem para obter \(h[-k]\)
- Obter \(h[n-k]\) deslocando a sequência refletida até \(k=n\)
- Multiplicar \(h[n-k]\) por \(x[k]\)
As propriedades definidas para a convolução são:
- Comutatividade: \((f * g)[n] = (g * f)[n]\)
- Distributividade sobre a adição)
- Associação em série (a própria convolução)
- Associação em paralelo (som a de sinais)
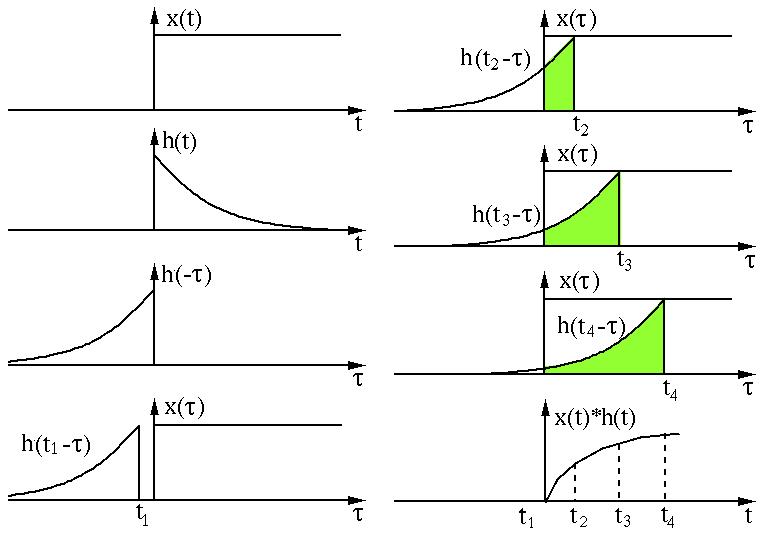
Figure 1: Exemplo de convolução contínua no tempo entre uma função exponencial descrescente e a função degrau.
No final geralmente temos um PG para se calcular. Onde pode ser uma PG infinita convergente, ou uma PG simples finita. Para as duas as fórmulas são conhecidas.
Exercício sobre convolução
Exercício 2.3: Encontre a resposta ao degrau dado a resposta ao impulso a seguir:
\[h[n] = a^{-n}u[-n] \quad 0 < a < 1 \]
Resposta: De acordo com a definição de soma de convolução na (Eq. 1), é importante lembrar também que a operação de convolução é um operador que suporta comutatividade. O que será importante nessa análise.
Podemos inicialmente analisar essa soma da seguinte maneira:
Se \(n < 0\) então, \(u[n -k] = 1\) para \(k \geq 0\). Não interessa para \(k < 0\) pois \(u[k] = 0\). Logo, reescrevendo a expressão temos que para \(n < 0\):
Onde \(\sum_{k=0}^\infty a^k\) é a progressão geométrica infinita, tal como \(0 < a < 1\), equivalente a \(\dfrac{1}{(1 - a)}\). Portanto, através do desenvolvimento anterior temos que para \(n < 0\):
Não podemos usar a mesma convolução acima definida entre \((x * h)[n]\) para \(n \geq 0\) devido ao fato que o resultante disso seria uma progressão geométrica condicionada da existência de seus termos somente para \(k \geq n\), do contrário o termo é nulo por conta da função degrau \(u[k -n]\). Nesse caso, é um grande problema pois \(\forall n \in \mathbb{Z}\) a sequência está definida e não incluindo todos os elementos na soma isto não será propriamente uma soma de progressão geométrica.
No entanto ao aplicar a propriedade da comutatividade da convolução podemos contornar este problema. Ao aplicar a propriedade de comutatividade, temos que para \(n \geq 0\):
Como \(k \leq 0 \Rightarrow -k \geq 0\), portanto a mesma relação de PG vale no último passo. Dessa maneira, finalmente temos que através de (Eq. 1) e (Eq. 1) a convolução desses dois sinais é dado como:
Relação: Transformada de Laplace e Convolução
A convolução e a transformada de Laplace possuí algumas propriedades interessantes, entre elas, durante a transformada de Laplace, a convolução se torna apenas uma multiplicação das transformadas de Laplace das funções individuais. No nosso contexto de PDS, sinais.
A Transformada de Laplace transforma um sinal dependente do tempo para o domínio da frequência. Como é um assunto muito extenso, com muitas propriedades e implicações, irei deixar isso de lado por enquanto. Talvez no livro eu ache mais algum contexto relevante para aplicação em PDS.
Dado que a Transformada de Laplace no tempo contínuo é dada como:
Equações de Diferenças
Equações de diferenças podem ser usadas para implementar sistemas que podem ter duração infinita ao impulso infinita ou simplesmente para o fazê-los de maneira mais eficiente.
Tendo o citado acima m mente, é importante comentar que existem dois tipos de sistemas LTI:
- FIR (finite-duration impulse response) \(\Rightarrow\) RI de duração finita;
- IIR (infinte-duration impulse response) \(\Rightarrow\) RI de duração infinita.
Sistemas FIR são sempre estáveis (RI tem sempre soma das magnitudes finita).
Nem todo sistema IIR é estável, \(|h[n]|\) deve ser absolutamente somável.
Um bom exemplo de IIR estável é a resposta impulso do último exemplo sobre convolução feito em Exercício sobre convolução.
A equação de recorrência
Uma implementação de sistema por equações de diferenças, tem sua representação numa equação de recorrência (recursiva). Um bom exemplo é uma implementação mais eficiente do acumulador, dado como: \(y[n] = x[n] + y[n-1]\).
Analogamente, é possível definir também a média móvel através de uma equação de recorrência:
\[h[n] = \dfrac{1}{M_2 + 1} (u[n] - u[n - M_2 -1])\]
Um problema tanto relevante é que como uma recorrência é definida em termo de valores já calculados, logo é necessário sabermos todos os valores para \(n' < n\) e então ser possível calcular a sequência. Logo uma equação de recorrência é sempre um sistema com memória (posso afirmar isso?).
Relação com equações diferenciais (caso contínuo)
As equações de diferenças são definidas no tempo discreto. O que conhecemos de equações diferenciais isto está definido no contexto do domínio contínuo. Mas as ideias entre ambas operações são muito semelhantes.
Solução homogênea(natural) e particular (forçada)
A solução homogênea, embora não necessária nesse curso, refere-se ao contexto de que um sistema possui uma condição inicial. A solução homogênea não depende da entrada, pois a entrada é zero. Isso é um ponto negativo em LTI, pois isso o torna um sistema variante no tempo e também não é linear. O que de fato não queremos.
Num contexto de circuítos elétricos, uma solução homogênea lembra problemas como exemplo o comportamento de um circuito RC (Resistor - Capacitor) em que sua energia inicial é não-nula.
A resposta forçada e particular é justamente a que temos interesse, na qual é 'forçado' um sinal em relação a resposta. Nesse caso a resposta particular é linear e invariante no tempo.
A solução geral da saída do sistema é descrita como:
\[ y[n] = y_h[n] + y_p[n] \]
Sendo que a equação para solução homogênea é a solução de:
\[ \sum_{k=0}^N a_k y[n-k] = 0 \]
Representação no domínio da frequência
Um sistema pode ser caracterizado por sua frequência, um exemplo é aplicar a entrada de \(x[n] = e^{jwn}\) para \(n \in (-\infty, \infty)\).
A resposta ao impulso para a entrada dada é:
É observável que o somatório entre parenteses nada mais é que uma constante. Pois não depende da entrada \(n\), ou seja não depende do tempo! No entanto, ela varia em torno da frequência, essa entidade é conhecida como resposta em frequência.
Essa propriedade ocorre pois a exponencial complexa é uma autofunção, sendo a autofunção a exponencial complexa que está fora do somatório e o próprio somatório no final o autovalor.
Uma propriedade importante é que durante a aplicação de um sistema em domínio da frequência, a frequência não muda, apenas a fase e a amplitude desse sinal. O que é uma propriedade muito desejada em projeto de filtros.
Resposta em frequência
Definição de resposta em frequência, como descrito na seção anterior, tem-se que:
Logo o sinal se torna:
Onde \(H(e^{j\omega})\) é o autovalor. Esta operação é periódica com período \(2\pi\).
Transformada de Fourier (TF)
A transforma de Fourier no contexto de processamento digital de sinais é usada para representar um sistema de domínio do tempo para domínio da frequência. Uma propriedade interessante é que a exponencial complexa é uma autofunção. Isso quer dizer que se um sinal de entrada é uma exponencial complexa, a saída do sistema será também uma exponencial complexa multiplicada por uma constante.
Isso simplifica todo o trabalho muito complicado de lidar com diferentes tipos de convolução de sinais discreto no tempo. Pois, ao transformar um sinal para o domínio da frequência usando a Transformada de Fourier, nosso sinal fica em função da frequência em relação a exponenciais complexas. Sendo assim, para aplicar um sistema temos apenas que lidar com operações simples de multiplicações de exponenciais complexas.
A transformada de Fourier de um sinal qualquer é dada para um sinal \(x[n]\):
Também conhecida como uma operação de análise.
Transformada de Fourier Inversa (TFI)
A operação de reconstrução do sinal, voltando ao domínio real e discreto é feito através de uma integral complexa. A transformada de Fourier é definida como \(\mathcal{F}: \mathbb{R} \rightarrow \mathbb{C}\) e \(\mathcal{F}^{-1}: \mathbb{C} \rightarrow \mathbb{R}\).
Sendo que a fórmula para síntese, reconstrução do sinal da a transformada de Fourier, é equivalente a:
Sendo que para nosso caso a entrada da transformação \(\mathcal{F}\) é discreta mas após a transformação é contínua e complexa!
Referências
- OPPENHEIM; ALAN, 1999, Discrete-Time Signal Processing 2nd Edition
- DINIZ; PAULO, 2010, Digital Signal Processing System Analysis and Design 2nd Edition